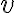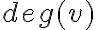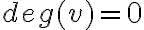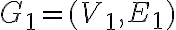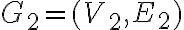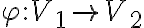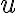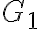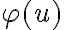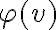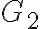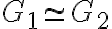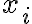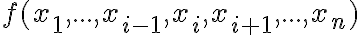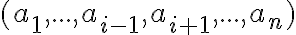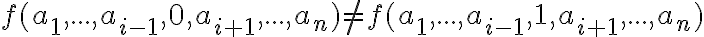Голосарій курсу
Огляд глосарія за абеткою
Спеціальні | А | Б | В | Г | Ґ | Д | Е | Є | Ж | З | И | І | Ї | Й | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Ь | Ю | Я | Все
І |
|---|
Ізольована вершина. | |
Ізоморфізм графів. | |
Інваріант.Інваріант – це властивість, яку довільні
ізоморфні графи або обидва мають, або обидва не мають. | |
Інцидентна вершина. | |
Інцидентні вершина та ребро у графі. | |
Істотна змінна. | |