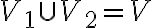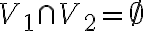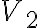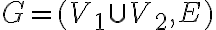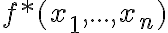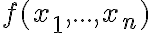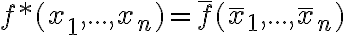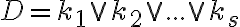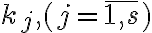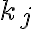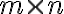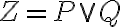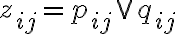Голосарій курсу

Граф $G=(V,E)$ називають дводольним, якщо множину його вершин $V$ можна розбити на дві підмножини  $V_1$  і  $V_2$ ,  що не перетинаються ( $V_1\cup V_2=V$, $V_1\cap V_2=\emptyset$), так, що кожне ребро з’єднує вершину з  $V_1$ і вершину з  $V_2$.  Іноді дводольний граф позначають як $G=(V_1\cup V_2, E)$ .

Двозв’язні графи – це зв’язні графи без точок з’єднання, відмінні від графа $K_1$.

Функцію  $f*({{x}_{1}},...,{{x}_{n}})$ називають двоїстою до функції $f({{x}_{1}},...,{{x}_{n}})$, якщо$f*({{x}_{1}},...,{{x}_{n}})=\overline{f}({{\overline{x}}_{1}},...,{{\overline{x}}_{n}})$.

Деревом називають зв’язний граф без простих циклів.

Диз’юнктивною нормальною формою (ДНФ) називають диз’юнкцію $D=k_1\vee k_2\vee ... \vee k_s$ елементарних кон’юнкцій  $k_j, (j=\overline{1,s})$, у якій  $k_j$ попарно різні.

Диз’юнкція булевих  $m\times n$ матриць $P$ та $Q$ – це $m\times n$  матриця $Z=P\vee Q$, елементи якої  $z_{ij}=p_{ij}\vee q_{ij}$, де  $i=\overline{1,m}$, $j=\overline{1,n}$.

Довжиною  орієнтованого шляху називають кількість дуг, з яких він складається.

Кількість елементів списку називають його довжиною.

Довжиною шляху в зваженому графі називають суму ваг ребер (дуг), які утворюють цей шлях.

Досконалою кон’юнктивною нормальною формою (ДКНФ) називають КНФ, у якої кожна елементарна диз’юнкція  $d_j, (j=\overline{1,s})$– конституента нуля.