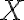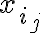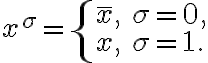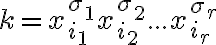Голосарій курсу

Граф, який має ейлерів цикл, часто називають ейлеровим графом.

Ейлеровим циклом у зв’язному мультиграфі $G$ називають простий цикл, який містить усі ребра графа.

Ейлеровим циклом у слабко зв’язному орієнтованому мультиграфі називають орієнтований простий цикл, який містить усі дуги графа.

Ейлеровим шляхом у зв’язному мультиграфі $G$ називають простий шлях, який містить усі ребра графа.

Формули називають еквівалентними (або тотожними, рівносильними), якщо вони реалізують рівні булеві функції.

Два елементи множини $A$, пов’язані відношенням еквівалентності, називають еквівалентними.

Елементарною диз’юнкцією називають вираз  $d=x_{i_1}^{\sigma_1}\vee x_{i_2}^{\sigma_2}\vee ... \vee x_{i_r}^{\sigma_r}$,  де $x_{i_j}, (j=\overline{1,r})$ – змінні з множини $X$, причому всі  $x_{i_j}$ різні. Тут $x^\sigma=\left\{ \begin{array}{ll} \overline{x}, & \sigma=0, \\ x, & \sigma=1. \\ \end{array} \right.$

Елементарною кон’юнкцією називають вираз  $k=x_{i_1}^{\sigma_1}x_{i_2}^{\sigma_2}...x_{i_r}^{\sigma_r}$, де $x_{i_j}, (j=\overline{1,r})$ – змінні з множини $X$, причому всі $x_{i_j}$  різні. Тут $x^\sigma=\left\{ \begin{array}{ll} \overline{x}, & \sigma=0, \\ x, & \sigma=1. \\ \end{array} \right.$