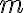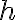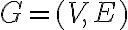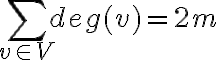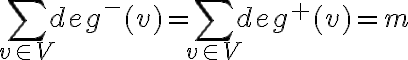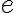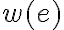Голосарій курсу
Огляд глосарія за абеткою
Спеціальні | А | Б | В | Г | Ґ | Д | Е | Є | Ж | З | И | І | Ї | Й | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Ь | Ю | Я | Все
З |
|---|
Завершене m-арне дерево. | |
Збалансоване кореневе m-арне дерево. | |
Зв'язний неорієнтований граф.Неорієнтований граф називають зв’язним, якщо будь-які дві його
вершини з’єднані шляхом. | |
Зв’язок між степенями вершин неорієнтованого графа та кількістю його ребер. | |
Зв’язок між степенями вершин орієнтованого мультиграфа та кількістю його дуг. | |
Зважений граф. | ||
Зважений орієнтований граф. | ||