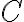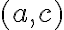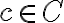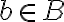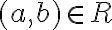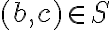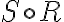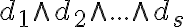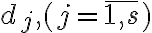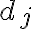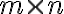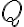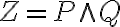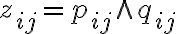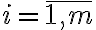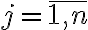Голосарій курсу
Огляд глосарія за абеткою
Спеціальні | А | Б | В | Г | Ґ | Д | Е | Є | Ж | З | И | І | Ї | Й | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Ь | Ю | Я | Все
К |
|---|
Каркасний підграф (фактор). | |
Клас еквівалентності за відношенням. | ||
Колесо. | |
Компоненти зв’язності (компоненти) графа.Незв’язний граф складається із двох або більше зв’язних підграфів, кожна
пара з яких не має спільних вершин. Ці зв’язні підграфи називають компонентами зв’язності або просто компонентами графа. | ||
Кон’юнктивна нормальна форма. | |
Кон’юнкція булевих матриць. | |
Конституента нуля. | |
Конституента одиниці. | |
Кореневе дерево.Дерево разом із виділеним коренем утворює орієнтований граф, який
називають кореневим деревом. | |
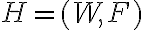
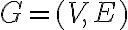
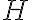
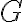
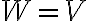
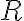
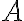
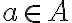
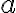
![[a]_R [a]_R](https://virt.ldubgd.edu.ua/filter/tex/pix.php/bb2c358e8734db68d89b1c519c66f37d.gif)
![b\in [a]_R b\in [a]_R](https://virt.ldubgd.edu.ua/filter/tex/pix.php/205b578e51e22dc95cf373ccdc8a1d3a.gif)