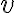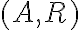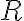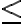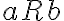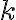Голосарій курсу

Вершини дерева, які не мають синів, називають листками.

Піддерево з коренем у вершині, яка являє собою лівого сина вершини $v$, називають лівим піддеревом у вершині  $v$. Якщо корінь піддерева – правий син вершини  $v$, то таке піддерево називають правим піддеревом у вершині   $v$.

Якщо внутрішня вершина впорядкованого бінарного дерева має двох синів, то першого називають лівим сином, а другого – правим.

Якщо $(A,R)$ – частково впорядкована множина, у якій будь-які два елементи порівнювані, то її називають лінійно, або тотально впорядкованою, а частковий порядок $R$ – лінійним, або тотальним порядком.

Лінійно впорядковану множину називають також ланцюгом.

Лінійний порядок $\leq$ називають сумісним із частковим порядком $R$, якщо з $aRb$ випливає $a \leq b$.

Граф, який не містить простих циклів і складається з $k$ компонент, називають лісом із $k$ дерев.