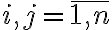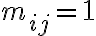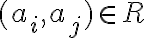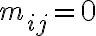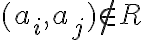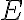Голосарій курсу
Огляд глосарія за абеткою
Спеціальні | А | Б | В | Г | Ґ | Д | Е | Є | Ж | З | И | І | Ї | Й | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Ь | Ю | Я | Все
М |
|---|
Максимальний елемент частково впорядкованої множини.Елемент частково впорядкованої множини називають максимальним, якщо він не менший за
будь-який елемент цієї множини. | |
Матриця інцидентності графа. | |
Матриця інцидентності орієнтованого графа. | |
Матриця суміжності графа. | |
Матриця суміжності орієнтованого графа. | |
Матриця, яка задає відношення. | |
Мінімальний елемент частково впорядкованої множини.Елемент називають мінімальним, якщо він не більший за будь-який елемент частково
впорядкованої множини. | |
Міст. | |
Монотонна елементарна кон'юнкція.Елементарну кон’юнкцію називають монотонною, якщо вона не містить
заперечень змінних. | |
Мультиграф. | |
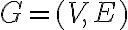
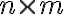
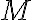

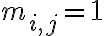
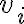
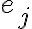
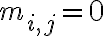
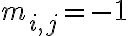
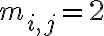
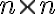
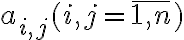
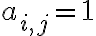
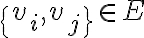
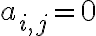
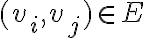
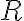
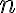
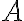
![M_R=[m_{ij}] M_R=[m_{ij}]](https://virt.ldubgd.edu.ua/filter/tex/pix.php/b56c060283ce6dc3e72a2324f60f45ac.gif)