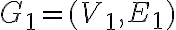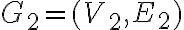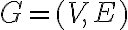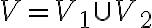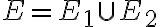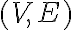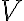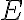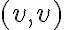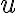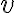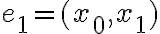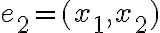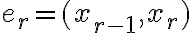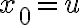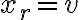Голосарій курсу

Об’єднанням двох простих графів $G_1=(V_1, E_1)$ та $G_2=(V_2, E_2)$ називають простий граф $G=(V, E)$ такий, що  $V=V_1\cup V_2$ , $E=E_1\cup E_2$.

Алгоритм обходу дерева в прямому порядку – ОПП(корінь)

·               Обробити(корінь)

·               Якщо лс(корінь) існує, то ОПП(лс(корінь))

·               Якщо пс(корінь) існує, то ОПП(пс(корінь))

Алгоритм обходу дерева у внутрішньому порядку – ОВП(корінь)

·               Якщо лс(корінь) існує, то ОВП(лс(корінь))

·               Обробити(корінь)

·               Якщо пс(корінь) існує, то ОВП(пс(корінь))

Алгоритм обходу дерева у зворотному порядку – ОЗП(корінь)

·               Якщо лс(корінь) існує, то ОЗП(лс(корінь))

·               Якщо пс(корінь) існує, то ОЗП(пс(корінь))

·               Обробити(корінь)

Орієнтованим графом називають пару $(V,E)$, де $V$ – скінченна непорожня множина вершин, а $E$ – множина впорядкованих пар елементів множини $V$. Елементи множини $E$ в орієнтованому графі називають дугами (орієнтованими ребрами). Дугу $(v,v)$ називають петлею.

Орієнтованим мультиграфом називають пару $(V,E)$, де $V$ – скінченна непорожня множина вершин, а $E$ – сім’я впорядкованих пар елементів з $V$.

Елементи (дуги) в $E$ в разі орієнтованого мультиграфа можуть повторюватись, такі дуги називають кратними.

Орієнтованим циклом називають орієнтований шлях, який з’єднує вершину саму із собою, тобто $u=v$.

Орієнтованим шляхом ( абр просто шляхом) з вершини $u$ в вершину $v$ називають скінчену послідовність дуг $e_1=(x_0,x_1)$,  $e_2=(x_1,x_2)$, ...,  $e_r=(x_{r-1},x_r)$, де $x_0=u$, $x_r=v$ , $r$ – натуральне число. Вершини $u$ та $v$ називають крайніми, а решту вершин шляху – внутрішніми.

Множину вершин, суміжних із вершиною $v$, будемо називати оточенням вершини $v$.