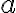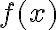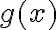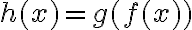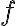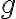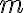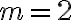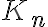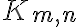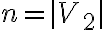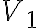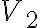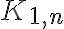Голосарій курсу
Огляд глосарія за абеткою
Спеціальні | А | Б | В | Г | Ґ | Д | Е | Є | Ж | З | И | І | Ї | Й | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Ь | Ю | Я | Все
П |
|---|
Петля.Петлі – ребра, які з’єднують вершину саму із собою. | |
Підграф. | |
Піддерево з коренем. | |
Підстановка функції в іншу функцію. | |
Повне m-арне дерево. | ||
Повний граф. | |
Повний дводольний граф. | ||
Позначений граф. | |
Поліном Жегалкіна. | |
Порівнювані елементи. | |