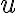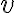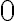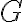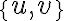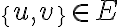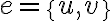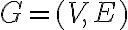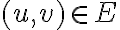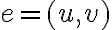Голосарій курсу

Функція може бути двоїстою до самої себе, тоді її називають самодвоїстою.

Орієнтований граф називають сильно зв’язним, якщо для будь-яких його різних вершин $u$ та $v$ існують орієнтовані шляхи від $u$ до $v$ та від $v$ до $u$. 

Отже, для сильної зв’язності орієнтованого графа повинна існувати послідовність дуг з урахуванням орієнтації від будь-якої вершини графа до будь-якої іншої.

Орієнтований граф називають слабко зв’язним, якщо існує шлях між будь-якими двома різними вершинами у відповідному йому неорієнтованому графі (тобто без урахування напрямку дуг).

Будь - яку скінченну послідовність елементів довільної природи будемо називати списком.

Степінь вершини в неорієнтованому графі – це кількість ребер, інцидентних цій вершині, причому петлю враховують двічі.

Найбільший із рангів елементарних кон’юнкцій, що входять у поліном, називають степенем полінома. За окремим означенням $0$ також уважатимемо поліномом Жегалкіна.

Дві вершини $u$ та $v$ в неорієнтованому графі $G$ називають суміжними, якщо існує ребро $\{ u,v\}$, тобто $\{ u,v\}\in E$. Якщо $e=\{ u,v\}$ – ребро, то вершини $u$ та $v$ називають його кінцями.

Нехай $G=(V,E)$ - орієнтований мультиграф.

Якщо $(u,v)\in E$, то вершину $u$ називають початковою (ініціальною), а вершину $v$ – кінцевою (термінальною) вершиною дуги $e=(u,v)$.

Вершини орієнтованого графа називають суміжними, якщо одна з них – початкова, а інша – кінцева для якоїсь дуги.

Дуги називають суміжними, якщо вони мають спільну вершину.

Два ребра називають суміжними, якщо вони мають спільний кінець.