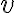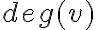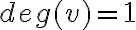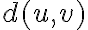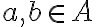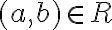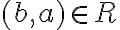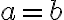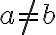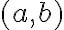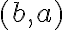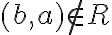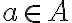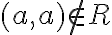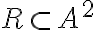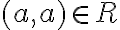Голосарій курсу
Огляд глосарія за абеткою
Спеціальні | А | Б | В | Г | Ґ | Д | Е | Є | Ж | З | И | І | Ї | Й | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Ь | Ю | Я | Все
В |
|---|
Висота кореневого дерева.Висотою кореневого дерева називають максимальний із рівнів його вершини. | |
Висяча (кінцева) вершина. | ||
Віддаль Геммінґа. | |
Віддаль між вершинами в неорієнтованому графі. | ||
Відношення антисиметричне. | |
Відношення асиметричне. | |
Відношення еквівалентності. | |
Відношення іррефлексивне. | |
Відношення на множині А. | |
Відношення рефлексивне. | |